En los sistemas asíncronos tipo compuerta, los elementos de almacenamiento requerido consisten en compuertas lógicas cuyo retardo de propagación hace posible el almacenamiento requerido. Así, un circuito secuencial asíncrono podría considerarse como un circuito combinacional con retroalimentación gracias a las retroalimentaciones entre compuertas lógica el circuito secuencial asíncrono podría volverse inestable ocasionalmente. El problema de inestabilidad impone muchas dificultades al diseñador.

El Método de Karnaugh es un método de simplificación de funciones mecánico; es decir, no hay que tener presente ninguna ley matemática presente. Nos permitirá simplificar funciones con dos, tres, cuatro, …variables de una forma sencilla.

Suponemos que tenemos una función F(A,B,C) de tres variables, cuya tabla de verdad es:

ABC	F
000	0
001	0
010	1
011	1
100	1
101	1
110	1
111	1

Si la desarrollamos por la primera forma canónica o de minitérminos, para ello tomamos aquellas entradas que nos hacen «1» la función :

F = A’BC’ + A’BC + AB’C’ + AB’C + ABC’ + ABC

Observamos, que cuando utilizamos minitérminos, las entradas con valor «0» están complementadas, y las entradas con valor «1» no están complementadas, es decir:

010 = A’BC’
Veremos como aplicando el método de Karnaugh podemos simplificar esta función.

Aplicamos Karnaugh para la tabla de verdad anterior, para ello dibujamos una tabla de la siguiente forma:

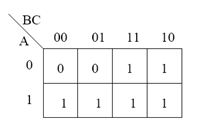
En cada casilla está colocado el valor de la función F, correspondiente a esa entrada.

En la tabla de verdad hay dos filas en las que F=0 y seis filas en las que F=1.

En el nuevo diagrama hay dos casillas con «0» y seis con «1». Hay dos filas, en la primera fila están todos los valores de F correspondientes a A=0, y en la segunda correspondientes a A=1.

Hay cuatro columnas, y el número que está en la parte superior de cada una de ellas nos indica los valores de las variables B y C en esa columna.
Así por ejemplo, si tomamos como referencia la casilla que está en la esquina inferior derecha, se corresponde con el valor que toma F cuando A=1, B=1 y C=0.
Entre dos casillas adyacentes cualesquiera, sólo varía una variable de entrada, quedando las otras dos con los mismos valores.
Si lo comparamos los valores de las variables correspondientes a la casilla anterior, vemos que sólo ha cambiado una de las tres variables, la C. Lo mismo ocurre si nos desplazamos a cualquier otra casilla adyacente.
Ahora vamos a ver una propiedad “mágica” de esta tabla.

Si obtenemos la primera forma canónica, obtenemos una función con seis términos. Vamos a fijarnos sólo en los términos que obtenemos si desarrollamos sólo dos casillas adyacentes, como por ejemplos las marcadas en gris en la siguiente tabla:

Los valores de las variables en estas casillas son: A=1, B=1, C=1 y A=1, B=1, C=0. Si obtenemos los términos de la primera forma canónica y los sumamos:

ABC + ABC’ = AB(C + C’) = AB

De esta manera, vamos a ver que pasa si tomamos los siguientes grupos:

y sumamos los términos de estos grupos:

Grupo 1:A’BC + A’BC’ = A’B(C + C’) = A’B
Grupo 2: AB’C’ + AB’C = AB’ (C’ + C) = AB’
Grupo 3: El que teníamos antes: AB

Por tanto, la función F₁ también la podemos expresar como suma de estos grupos:

F₁ = A’B + AB’ + AB
Todavía más simplificada que la anterior. Pero… ¿Es la más simplificada?. No, todavía podemos simplificarla más. ¿Por qué no podemos tomar 2 grupos de 4 casillas adyacentes?. Tomemos los grupos siguientes:

Las nuevas expresiones de los grupos son:

Grupo 1: A’B + AB = B (A’ + A) = B
Grupo 2: Igual que antes: A

Por tanto, la nueva función F₃ simplificada es:

F₃ = A + B

Criterio de máxima simplificación:

Para obtener una función que no se puede simplificar más, hay que tomar el menor número de grupos con el mayor número de «1» en cada grupo.

Nos damos cuenta, que las tres funciones obtenidas son esquivalentes, pero la más simplificada es F₃.

F₁ = A’B + AB’ + AB

F₂ = A’B + A

F₃ = A + B

Por lo que deducimos que cuanto mayor sea el conjunto de «1» «adyacentes», mayor será la simplificación. Pero cuidado, sólo se pueden hacer grupos de 2 elementos, 4 elementos, 8 elementos, … y siempre que éstos sean adyacentes. (FUENTE : ikastaroak.ulhi.net )

¿Que es un flip flop?

El flip flop es el nombre común que se le da a los dispositivos de dos estados (biestables), que sirven como memoria básica para las operaciones de lógica secuencial.

Son dispositivos con memoria mas comúnmente utilizados. Sus características principales son:

Asumen solamente uno de dos posibles estados de salida.
Tienen un par de salidas que son complemento una de la otra.
Tienen una o mas entradas que pueden causar que el estado del Flip-Flop cambie.

Los flip flops se pueden clasificar en dos:

Asíncronos: Sólo tienen entradas de control. El mas empleado es el flip flop RS.
Síncronos: Ademas de las entradas de control necesita un entrada sincronismo o de reloj.

Flip-Flop R-S (Set-Reset)

Utiliza dos compuertas NOR. S y R son las entradas, mientras que Q y Q’ son las salidas (Q es generalmente la salida que se busca manipular.)
La conexión cruzada de la salida de cada compuerta a la entrada de la otra construye el lazo de reglamentación imprescindible en todo dispositivo de memoria.

Flip-Flop T

El Flip-flop T cambia de estado en cada pulso de T. El pulso es un ciclo completo de cero a 1. Con el flip flop T podemos complementar una entrada de reloj al flip flop rs.

La siguiente tabla muestra el comportamiento del FF T y del FF S-R en cada pulso de t.

Flip-Flop J-K (Jump-Keep)

El flip-flop J-K es una mezcla entre el flip-flop S-R y el flip-flop T.
A diferencia del flip flop RS, en el caso de activarse ambas entradas a la vez, la salida adquiere el estado contrario al que tenía.