Concepto:

Circuito combinacional, es un circuito cuya salida depende solamente de la «combinación» de sus entradas en el momento que se está realizando la medida en la salida.

Operación

La operación de los circuitos combinacionales se entienden escribiendo las ecuaciones booleanas y sus tablas de verdad.

Todos los circuitos combinacionales pueden representarse empleando álgebra de Boole a partir de su función lógica, generando de forma matemática el funcionamiento del sistema combinacional.

. Estas operaciones se pueden combinar formando funciones más complejas. Así, el siguiente esquema se define por la función indicada debajo del mismo.

Ejemplo de ecuación booleana: F = A . B + A . B

Análisis

El comportamiento de los circuitos combinacionales sólo depende de las señales de entrada en un instante determinado, y no de la secuencia de entradas, es decir, de la historia del circuito.
Una posible definición de estos estados sería la siguiente:

El estado transitorio es aquel espacio temporal que va desde el cambio de las entradas hasta que la salida se estabilice.

El estado estacionario es aquel espacio temporal que va desde la estabilización del circuito lógico hasta que las entradas vuelvan a cambiar. ( fuente : ecured.cu )

TABLA DE LA VERDAD

Resultado de imagen de CIRCUITOS COMBINACIONALES DE LA VERDAD

Formas canónicas (álgebra de Boole)

En Álgebra booleana, se conoce como término canónico de una función lógica a todo producto o suma en la cual aparecen todas las variables en su forma directa o inversa.
Una Función lógica que está compuesta por operador lógico puede ser expresada en forma canónica usando los conceptos de minterm y maxterm. Esto permite un mejor análisis para la simplificación de dichas funciones, lo que es de gran importancia para la minimización de circuitos digitales. ( fuente : es.wikipedia.org)

Resultado de imagen de FUNCION CANONICA — Indexando minitérminos

Minitérminos

un minitérmino es una expresión lógica de n variables consistente únicamente en el operador conjunción lógica (AND) y el operador complemento o negación (NOT).

Indexando minitérminos
En general, uno asigna a cada minterm (escribiendo las variables que lo componen en el mismo orden), un índice basado en el valor binario del minterm.

Un término negado, como {a’} es considerado como el número binario 0 y el término no negado {a} es considerado como un 1.

Función equivalente

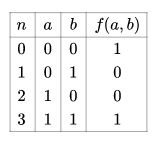
Si tenemos una tabla de verdad de una función lógica: f(a,b), es posible escribir la función como «suma de productos».

Observamos que las filas con resultado ‘1 son la primera y la cuarta, entonces podremos escribir f como la suma de los minitérminos: f(a,b)=m0+m3

Si queremos verificar esto: f(a,b)=m0+m3=(a’b’)+(ab)

{\displaystyle f(a,b)=m_{0}+m_{3}=(a'b')+(ab)}

Maxitérminos

Un maxitérmino es una expresión lógica de n variables que consiste únicamente en la disyunción lógica y el operador complemento o negación. Los maxterms son una expresión dual de los minitérminos. En vez de usar operaciones AND utilizamos operaciones OR y procedemos de forma similar.

Dualización

El complemento de un minterm es su respectivo maxitérmino. Esto puede ser fácilmente verificado usando la Ley de De Morgan.
Por ejemplo:
(a’b)’=a+b’

Indexando maxitérminos

Para indexar maxitérminos lo haremos justo de la forma contraria a la que seguimos con los minterms. Se asigna a cada maxterm un índice basado en el complemento del número binario que representa (otra vez asegurándonos que las variables se escriben en el mismo orden, usualmente alfabético).

Se puede ver fácilmente que un maxitérmino sólo da como resultado un cero para una única entrada de la función lógica. Por ejemplo, el maxitérmino 5, a’+b+c’, es falso solo cuando a y c son ciertos y b es falso – la entrada a = 1, b = 0, c = 1 da como resultado un cero.